On Players Evaluation - Part III (Teams Elo)

Part I.

Part II.

Sherlock Holmes and Dr. Watson are camping in the countryside.

In the middle of the night Holmes wakes up Watson:

'Watson, what do you think these stars are telling us?

'Geez, Holmes, I don't know, maybe it's going to be a nice weather tomorrow?

'Elementary, Watson! They are telling us our tent has been stolen!

Iconic Soviet joke.

Estimating a hockey player via Elo ratings is a highly complex task. Therefore, we shall wield the dialectic approach of getting from the simpler to the more complicated, and will tackle a seemingly simplistic task first. Let's work out the Elo ratings for the NHL teams as a whole first. After all, it's the teams who compete against each other, and the outcome of this competition is a straightforward result.

So, let's examine a match between Team A and Team B. They have ratings R_a and R_b. These ratings, or, more precisely, their difference R_a-R_b, defines the expected results E_a and E_b on the scale from 0 to 1. The teams play, one wins (S=1), another loses (S=0). To adapt this to the Elo scale, let's consider win 1 point, loss 0 point. The new ratings R_a^' and R_b^' will be (K is the volatility coefficient):

Outcome	Sa	Sb	Sa-Ea	Sb-Eb	dRa	dRb	Ra'	Rb'
Team A Wins	1	0	1-Ea	-Eb	K-K*Ea	-K*Eb	Ra+K-K*Ea	Rb-K*Eb
Team B Wins	0	1	-Ea	1-Eb	-K*Ea	K-K*Eb	Ra-K*Ea	Rb+K-K*Eb

and the teams are ready for usage in the next meeting with their new ratings R_a^' and R_b^', reciprocally.

'Wait!', will ask the attentive reader, 'Not all possible outcomes are listed above! What about the OT/SO wins where both teams get some points.' And he will be correct. In these cases we must admit that the loser team scores 0.5 points, so unlike a chess game where the sum of the results is always 1, in the NHL hockey the total sum of results varies and can be either 1 or 1.5. Note, were the scoring system 3-2-1-0, then we could scale the scores by 3 rather than by two and get the range 1-⅔-⅓-0 where every result sums to 1. Alas, with the existing system we must swallow the ugly fact that the total result may exceed 1, and as the result the ratings get inflated. Which is a bad thing, sure.

Or is it? Remember, the Elo expectation function only cares about the differences between ratings, not their absolute values. And all teams' ratings get inflated, so all absolute values shift up from where they would've been without the loser's point. Whom would it really hurt? The new teams. Naturally, we must assign an initial rating to every team at the starting point. One way could be assigning the average rating of the previous season to the new team. But we prefer a different and a much more comprehensive solution. We claim that since the teams that at the start of the next season are different enough beasts from those that ended the previous ones, so that the Elo ratings should not carry over from season to season at all! Therefore all the teams start each season with a clean plate and an identical Elo rating R_o.

Once again, the attentive reader might argue, 'What about mid-season trades and other movements?' Well, dear reader, now you have a tool to evaluate impact of the moves on the team. If there is a visible tendency change, you can quite safely associate it with that move. Overall, the 82 game span is huge to soften any bends and curves in the progression of the Elo ratings along the season.

Speaking of game spans, we must note one more refinement being done to the ratings. In the chess world, the ratings of the participants are not updated throughout the length of the event, which is usually 3-11 games. The ratings of the participants are deemed constant for the calculation of rating changes, which accumulate, and the accumulation is actually the rating change of each participant. We apply a similar technique for the teams' Elo calculations: we accumulate the changes for the ratings for 5 games for each team and "commit" the changes after the five-game span. The remainder of the games is committed regardless of its length, from 1 to 5. Why 5? We tried all kinds of spans, and 5 gave the smoothest look and the best projections.

Now, as a demonstration, let's show how we calculate the possible rating changes in the much anticipated game where Minnesota Wild is hosting Columbus Blue Jackets on December, 31st, 2016:

R_cbj = 2250, R_min = 2196, E_cbj = 0.577, E_min = 0.423, K = 32 (standard USCF).

Outcome	Scbj	Smin	S-Ecbj	S-Emin	dRa	dRb	Ra'	Rb'
CBJ W Reg	1	0	0.423	-0.423	+13.53	-13.53	2263.53	2182.47
CBJ W OT	1	0.5	0.423	0.077	+13.53	+2.47	2263.53	2198.47
MIN W OT	0.5	1	-0.077	0.577	-2.47	+18.47	2247.53	2214.47
MIN W Reg	0	1	-0.577	0.577	-18.47	+18.47	2231.53	2214.47

Note: MIN gains rating when it gets a loser's point.

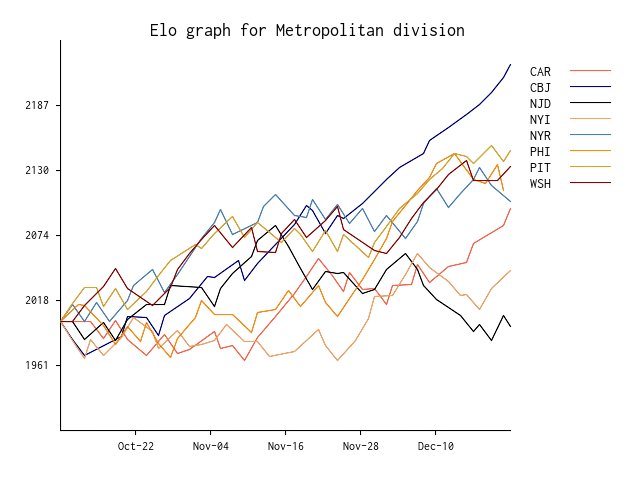
Here is a dynamic of Elo changes (without five game accumulation) for the Metropolitan Division, as an example.

See more detailed tables on our website: http://morehockeystats.com/teams/elo

Ok, we got the ratings, we got the expected results, can we get something more out of it?

To be continued...

Happy New Year to everyone!